
要科学规划管理类数学复习,首先需要清晰掌握考点的分布规律。通过对近年真题的系统统计(样本覆盖完整命题周期),我们整理出各章节的考查频次图谱,为考生呈现直观的考点分布全景。
从统计图表(如图1所示)可以观察到,应用题在历年考题中始终占据比重,年均考查量稳定在6至8题区间。这一现象与管理类考试的应用导向密切相关——应用题能有效检验考生将数学知识转化为实际问题解决能力的水平。紧随其后的是方程函数不等式、平面几何、解析几何和概率四大模块,这四个章节的年考查量基本维持在2至3题,构成了试卷的核心知识框架。
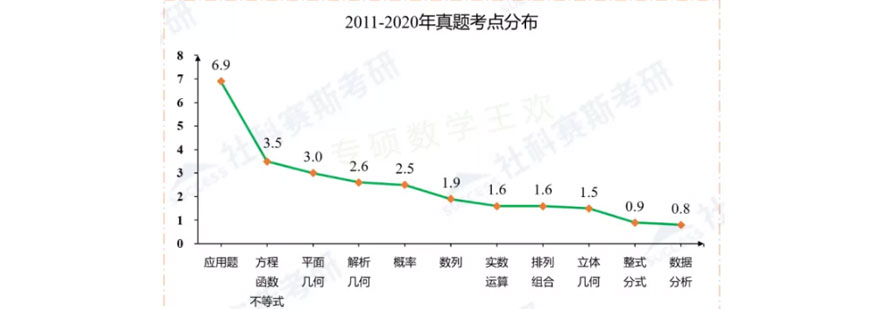
数列、实数运算、排列组合和立体几何的考查频次相对稳定,年平均1至2题。值得注意的是立体几何自纳入考试大纲以来,保持了连续考查的态势;数据分析模块早期涉及较少,但近年表现出明显的稳定化特征,年固定考查1题。整式分式作为基础章节,虽然直接命题较少(0至1题),但其知识内核深度渗透于其他章节的综合题中,是构建解题逻辑的重要工具。
进一步聚焦近六年(命题体系成熟期)的统计数据(如图2所示),可以发现各章节的考查频次呈现更强的稳定性。方程函数不等式、平面几何、解析几何和概率的题量波动幅度控制在±1题范围内;数据分析模块从早期的偶发考查发展为年固定1题的常规考点;应用题虽有小幅下降趋势,但仍以绝对优势保持着占比。
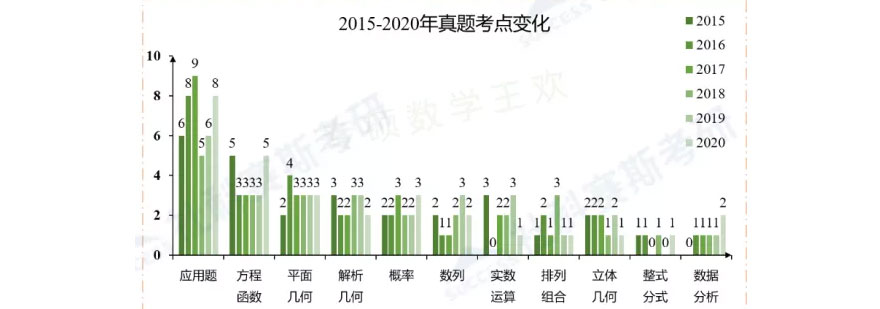
关于难度分布,近年真题中每年难题数量基本维持在1至2题。值得关注的是命题重点的迁移——早期数列曾连续多年作为难题集中区,而近年函数和解析几何逐渐成为命题人设置难度梯度的主要载体。需要特别说明的是,这并不意味着函数和解析几何只考难题,这两个章节在简单题和中档题中同样保持着较高的出镜率,考生需全面掌握其知识体系。
随着考试体系的不断成熟,管理类数学的命题方向呈现出显著的趋势性特征。深入理解这些变化,有助于考生把握复习的针对性和前瞻性。
条件充分性判断中,"确定性问题"的出现频率和命题深度均有明显提升。这类题型要求考生判断给定条件是否能唯一确定结论,其核心在于逻辑推理而非单纯计算。统计显示(如图3所示),近六年此类题型年均考查2至3题,且命题思路呈现出显著的延续性——出题人常对经典思路进行改编复用。
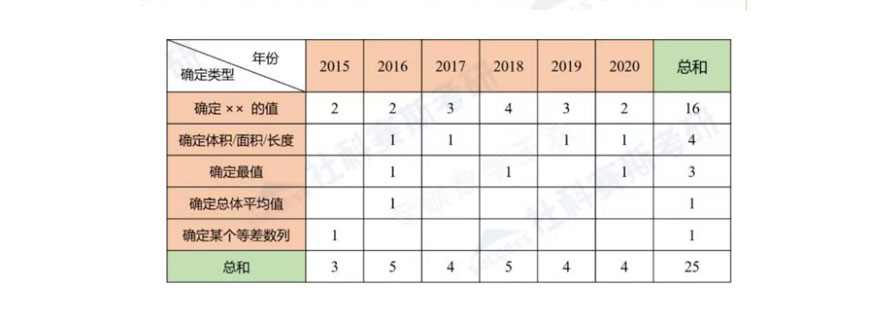
例如2015年和2020年的真题虽背景不同,但核心逻辑高度一致:当条件能推出唯一解时选C,推出多解时选E。考生在练习中应注重积累此类题型的典型模式,建立"条件-结论"的确定性分析框架。以下是常见的确定性问题类型示例:
与传统数学题侧重计算不同,近年真题中纯文字描述的题目占比显著增加。这类题目要求考生在理解文字信息的基础上,提炼数学模型,更强调对知识本质的理解而非机械运算。
以等差数列前n项和为例,2014年真题需要通过计算验证S₉=9a₅,而2018年同考点题目则直接考查"前n项和与等差中项关系"的本质理解,考生只需掌握Sₙ=n·aₘ(当n=2m-1时)的核心规律即可快速解题。这种考查方式既优化了试卷的时间分配,又深化了对数学思维的考查。
近三年真题中,早期较少涉及的"冷门考点"呈现出明显的回归趋势:2018年考查无穷等比数列求和,2019年出现余弦定理应用,2020年同时涉及周期数列和柯西不等式。这一变化提示考生,备考范围需覆盖考试大纲的全部知识点,避免因知识盲区导致失分。
结合上述考情分析,为帮助考生实现高效备考,我们提出以下针对性建议:
无论对某一章节的熟悉程度如何,都应简单题和中档题的解题能力。例如即使对立体几何不够擅长,也需掌握基本体积公式和空间几何关系的分析方法,确保在基础题中得分。
每套试卷中,难题、冷门题和怪题的总量通常不超过3题。建议优先基础题和中档题的正确率,有余力时再进行难题专项突破,避免因过度纠结偏题影响整体得分。
建议整理近十年真题中的确定性问题,建立专属题库。通过对比分析,总结"条件充分性判断"的常见逻辑模式(如唯一解判定、多解排除等),形成条件反射式的解题思维。
摒弃"死记硬背公式"的复习方式,注重推导过程和原理理解。例如掌握等差数列前n项和公式时,需理解其与等差中项的内在联系;学习概率模型时,要明确每种概率类型的适用场景。只有真正理解知识本质,才能在文字题和综合题中灵活运用。
管理类数学的备考本质上是对"数学思维"和"应试策略"的双重修炼。通过把握考点分布规律、顺应命题趋势变化、执行科学备考策略,考生完全有能力在有限时间内实现成绩的显著提升。